2022华为软件精英挑战赛，最优美代码赛队分享解题方案

5月21-22日，2022第八届华为软件精英挑战赛-“普朗克计划”总决赛及颁奖典礼在深圳成功举办。大赛吸引了来自国内外826所高校、3291支队伍、2万余名大学生报名参赛，历时两个多月的激烈角逐，经过八大赛区区域初赛、区域复赛、全球总决赛等环节的层层考验，最终，9支优秀队伍凭借优异表现分享了66万元总奖金池。其中，来自粤港澳赛区的“路路的小跟班”队，赢得“最优美代码奖”，赛队撰文分享其参赛体验，包括解题思路、比赛收获以及把代码做到“最优美”的技巧等。

1 比赛初衷

参加华为软件精英挑战赛的初衷是为了通过比赛提高自身的编程能力，开阔个人的眼界。通过不断的挑战不同的难题，提升问题的解决能力。同时通过比赛积累竞赛经验，在各种比赛中赢得更多的奖金。

2 赛题背景

提升用户体验的同时降低运营成本是云服务竞争力的关键。在视频直播场景中, 网络成本是影响服务成本的关键因素之一, 不同的流量调度方案会产生不同的网络使用成本。

本届赛题以华为云视频直播服务流量调度问题为基础, 并进行一定的抽象、调整和简化。参赛选手需要设计高效的调度算法, 在满足客户要求的前提下, 通过对流量的合理调度, 最小化网络使用成本。赛题中的流量调度示意图如Figure 1所示。

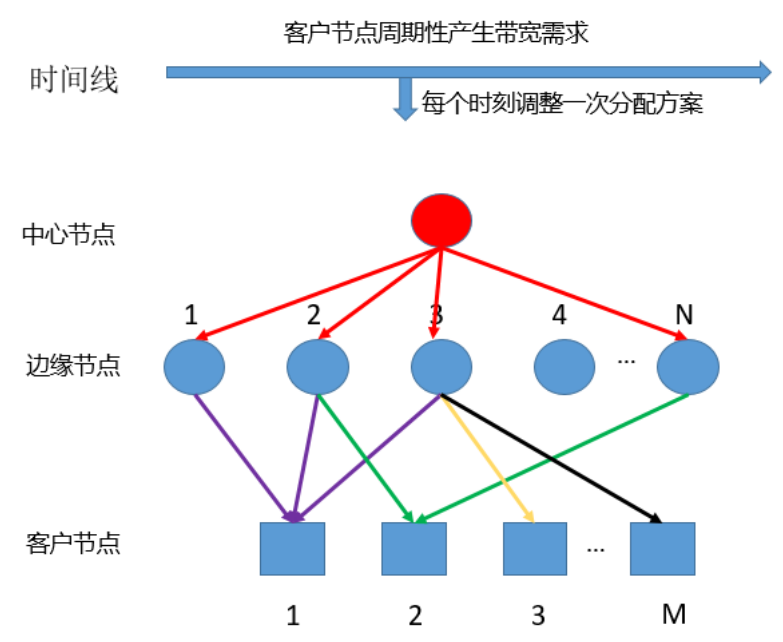
Figure 1: 流量调度示意图

3 解题思路

对于此类优化问题，我们首先需要针对问题寻找一个合法的初始解，然后再对初始解进行优化得到一个更优的解。

3.1 初始解的求解思路

初始解决定了最终的解决方案的下限，由于赛题限制了运行时间为300s，因此本次比赛最重要的一步是获得一个较好的初始解。我们的初始解求解方案包括了对数据流削峰，边缘节点带宽均衡化，以及使用成本公式进行流的分配三步。

3.1.1 数据流削峰处理

根据赛题描述中的单个边缘节点的成本计算方法，可以知道边缘节点带宽大于其P95 带宽值的时刻属于免费时刻，可以最大程度的利用。而客户节点的流在每一个时刻的总量是不同的，通常会存在明显的峰值，为了能够在时间维度上，对整体的数据流做一个削峰处理，我们利用每一个边缘节点的拥有的免费时刻来进行数据流的削峰，在具体的免费时刻选择上，我们通过计算边缘节点在每个时刻承载的流量和排序，选择前5% 时刻作为免费时刻，然后尽可能利用该时刻边缘节点的带宽装填数据流。在边缘节点排序上，我们尝试了多种排序方式，包括根据边缘节点连接的客户数量，边缘节点总容量，以及二者加权的方式进行排序。Figure 2是边缘节点经过削峰处理后在整体时间维度上的带宽使用情况。

Figure 2: 边缘节点95 百分位带宽

3.1.2 边缘节点带宽均衡化

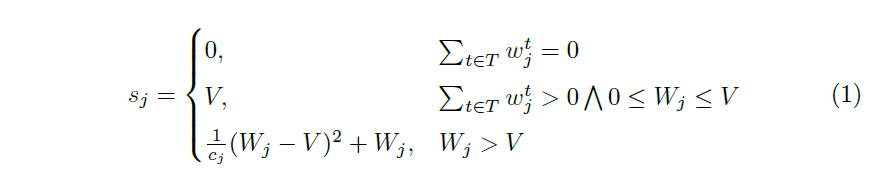
公式1定义了第j 个边缘节点的成本计算方式，观察可知边缘节点的成本与该节点的承载量并不是线性的，在边缘节点的P95 带宽超过边缘节点成本调整参数V 后，边缘节点的成本将随着承载量的增大以平方倍数增加。因此需要将数据流均衡分布到不同的边缘节点上，以减少惩罚。

在方案设计上，我们采用了一种均衡化方法，如Figure 3所示。通过尽可能的将数据流均匀的分布到不同的边缘节点上，以避免单个边缘节点承载量过高带来的额外惩罚。这里的难点在于，对于每个边缘节点，应该分配多少数据流总量。我们通过计算边缘节点在整个时间线上，每一个时刻应该承担的数据流总量，具体方法是将数据流的大小平摊到数据流能够分发的所有边缘节点上，然后将每一个边缘节点每一个的能够连接到的用户节点的数据流平均化求和，并进行排序，取最大值作为整个时间序列上该边缘节点的分发量。在边缘节点的选择顺序上，我们采用了第一步相同的排序思路，尽可能优先选择连接用户节点数较多以及容量较大的边缘节点。

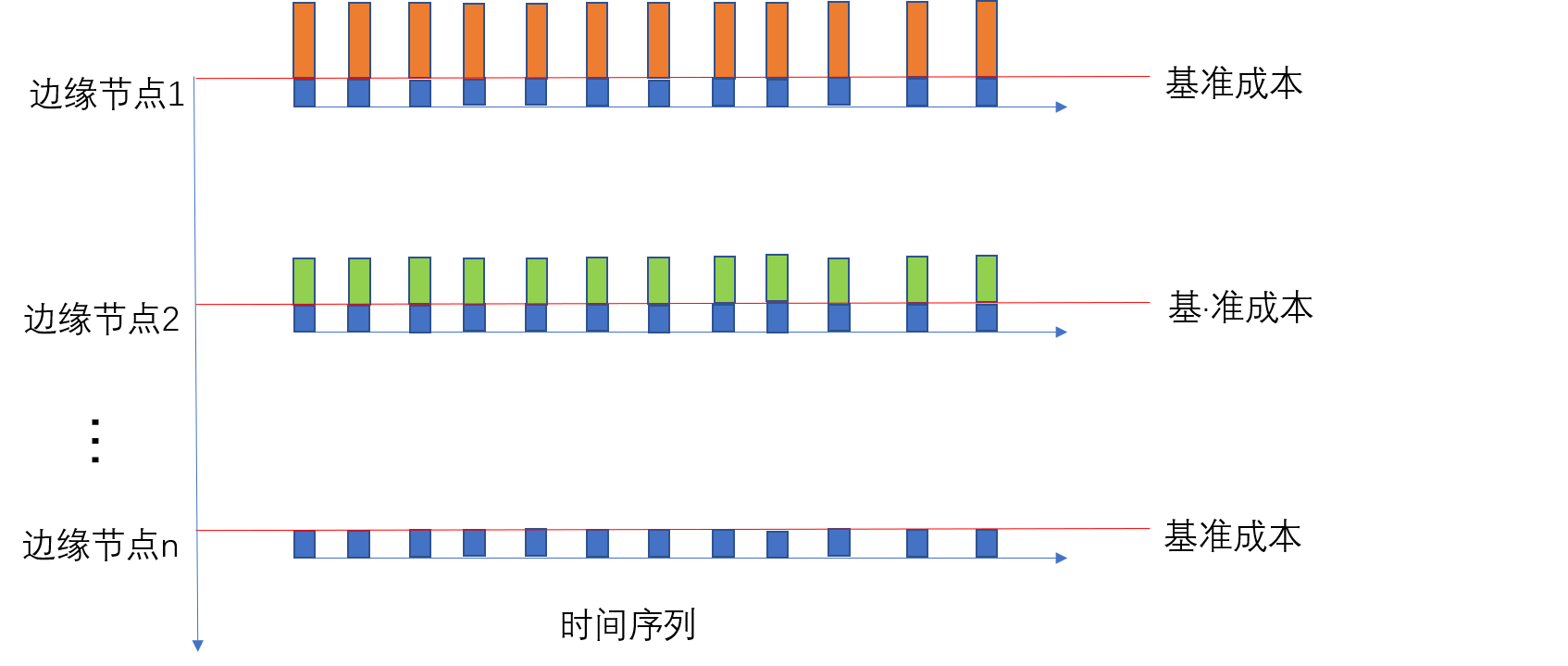
Figure 3: 边缘节点流量均衡化

3.1.3 使用成本公式进行剩余流的分配

经过上述两步，依然会剩下部分用户节点的流未进行分配，针对这部分流，我们采取流选边缘节点的方法，在边缘节点的选择上，使用公式2计算放入当前数据流后，中心节点成本与边缘节点成本增加最少的边缘节点，将数据流分配给该边缘节点。根据边缘节点和中心节点的成本计算出单个流增加成本最少的最优的边缘节点，并将该流放置到最优边缘节点。

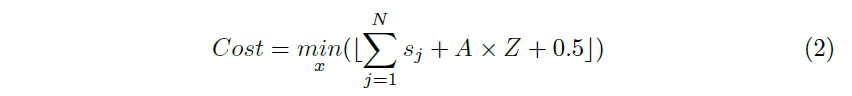
对于这个赛题而言，仅采用上述三步并不能保证有可行解，对于严格的数据，可能需要加上数据流迁移等操作得到合法解决方案。但在实际的数据集测试中，我们仅采用上述三步就已经产生了一个合法的可行解。

3.2 优化初始解的思路

如公式2所示，赛题的目标函数由中心节点成本和边缘节点成本两部分组成。为了简化模型，我们通过约束将多目标优化问题简化成单一目标优化问题，因此我们优化初始解的核心思路是通过约束其中一种成本不增加的同时降低另外一种成本，包含两个方向：

• 边缘节点的成本优化。通过约束中心节点成本不增加的同时使得边缘节点的成本降低；

• 中心节点的成本优化。通过约束边缘节点成本不增加的同时使得中心节点的成本降低。

3.2.1 边缘节点的成本优化

边缘节点的成本是一个分段函数，根据其P95 带宽使用不同的方式计算成本，其分段点是边缘节点成本调整参数V，在我们的理解中这是一种变相的开机成本。针对边缘节点的成本计算方式，我们设计了两种方案来优化边缘节点的成本，一是将边缘节点A 在其P95 时刻承载的流迁移至边缘节点B 后，边缘节点A 的边缘成本降低，而中心成本和边缘节点B 的成本不增加，下称“边缘迁移”；二是将边缘节点A 所有时刻承载的流均迁移至对应时刻的其他边缘节点，消除边缘节点A 的开机成本的同时使得中心成本和其他边缘节点的

边缘成本不增加，下称“腾空边缘节点”。

3.2.1.1 边缘迁移

边缘迁移主要用于降低边缘节点的P95 带宽，以达到降低边缘成本的效果，边缘迁移的算法框架见Algorithm 1。在边缘迁移的算法框架中，首先获得遍历边缘节点的顺序，遍历的顺序比较灵活，可用的排序指标包括边缘节点的成本，P95 带宽和P95 带宽时刻的梯度等，这里使用的是边缘节点的成本。在遍历边缘节点及其流量时刻的过程中，我们针对边缘迁移的目的设定了两个提前跳出循环的条件，具体可见代码及注释。最后则是边缘迁移的核心MigrateFromSiteForSiteCost 函数，它通过遍历对应时刻的边缘节点所承载的所有流，为这些流找到符合约束的迁入边缘节点。在我们的实现中，设置的约束包括以下三点：

• 迁入节点是非空节点。迁入节点不能在所有时刻都没有承载过流量。

• 待迁出流量不增加迁入节点的P95 带宽。待迁出流量带来的带宽以及缓存量不能增加迁入节点的P95 带宽。

•迁移后该时刻的中心成本不增加。迁出节点降低的中心成本不低于迁入节点升高的中心成本，即迁移后该时刻的中心成本不增加。

3.2.2 腾空边缘节点

为了降低开机成本V，我们设计了腾空边缘节点的操作。算法的主要约束与边缘迁移类似，不同之处在于腾空边缘节点的操作需要边缘节点在所有时刻承载的流量都可以迁出时我们才执行“腾空”操作。

3.3 中心节点的成本优化

观察中心节点的成本计算方式，易得核心优化思路是尽可能地将同一时刻同一类型的流量放在同一个边缘节点，下称“流量聚合”。为了实现流量聚合，我们设计了“中心迁移”算法，算法框架见Algorithm 2。中心迁移算法的整体框架与边缘节点类似，最主要的区别在于改变了迁移的约束条件，中心迁移的

约束条件包含以下三点：

• 迁入节点是非空节点。迁入节点不能在所有时刻都没有承载过流量。

• 待迁出流量不增加迁入节点的P95 带宽。待迁出流量带来的带宽以及缓存量不能增加迁入节点的P95 带宽。

• 迁移后中心带宽降低。迁移后，迁出节点减少的中心带宽需要大于迁入节点增加的中心带宽。

4 比赛收获

在本次比赛中，比较高兴的是我们获得了最优美代码奖，比较遗憾的是最终因为一个题意理解错误产生的BUG 失去了更进一步的机会。不过这次比赛收获颇丰，不但认识到自身的不足，而且认识了很多新的朋友。这不仅是一次比赛，更是一场旅行，感谢华为主办方的悉心安排，感谢工作人员在比赛过程中辛勤付出，感谢小伙伴之间的思维碰撞，希望未来仍有机会与大家相聚。

5 对于“最优美代码”的理解

软挑是一个团队比赛，为了减少沟通成本和提高编码效率，我们队伍主要规范了代码的可读性和可维护性。

5.1 可读性

在团队协作中，让队友快速读懂你的代码是非常重要的，为此我们队伍统一使用Google C++ 编程风格。团队成员统一编程风格并遵守约定意味着可以很容易根据“模式匹配”规则来推断各种标识符的含义。我们的编码风格如图4所示。

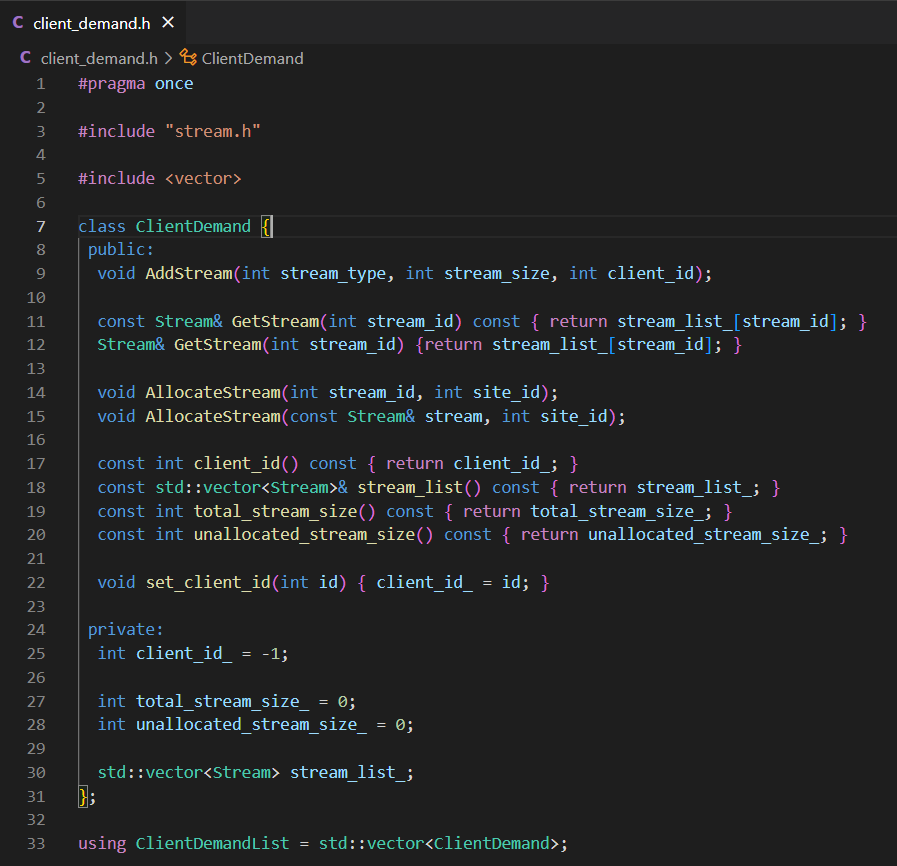Figure 4: 统一的编码风格

5.2 可维护性

软挑的正式赛是需要现场编码新需求的，因此代码的可维护性尤为重要。在编码过程中，我们尽量保持方法的原子性，提高代码内聚，并将实现的功能模块化，做到即插即用。如图5所示，我们对赛题进行了抽象和封装，设计出对应的数据结构。同时，我们将诸如将流在节点之间进行迁移的通用操作解耦出来，提高代码的内聚性，使得类似的功能能够即插即用。当然，我们也在一些关键点使用assert 等工具进行判断，提高代码的测试效率。

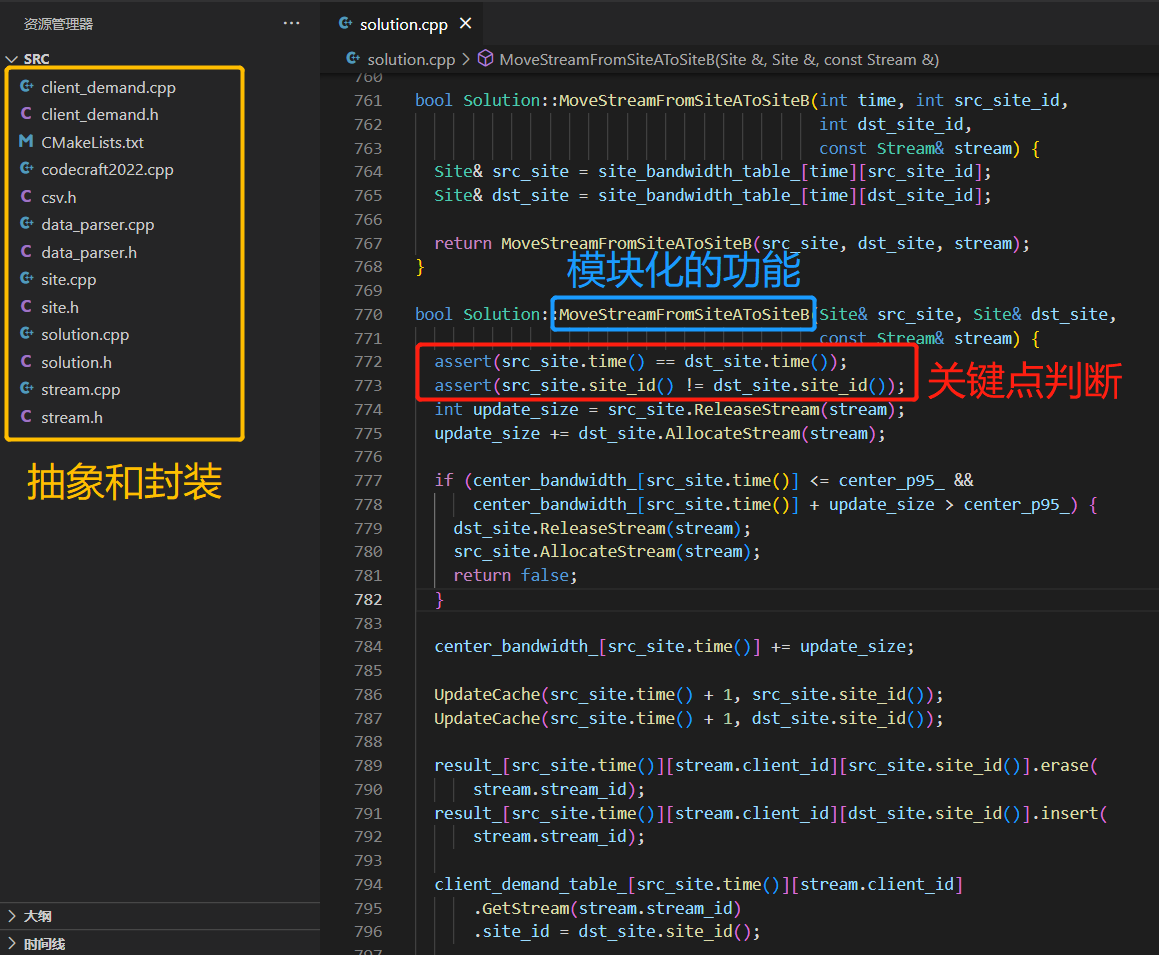
Figure 5: 提高代码的可维护性

生成海报

免责声明：本网站内容主要来自原创、合作伙伴供稿和第三方自媒体作者投稿，凡在本网站出现的信息，均仅供参考。本网站将尽力确保所提供信息的准确性及可靠性，但不保证有关资料的准确性及可靠性，读者在使用前请进一步核实，并对任何自主决定的行为负责。本网站对有关资料所引致的错误、不确或遗漏，概不负任何法律责任。任何单位或个人认为本网站中的网页或链接内容可能涉嫌侵犯其知识产权或存在不实内容时，应及时向本网站提出书面权利通知或不实情况说明，并提供身份证明、权属证明及详细侵权或不实情况证明。本网站在收到上述法律文件后，将会依法尽快联系相关文章源头核实，沟通删除相关内容或断开相关链接。